Λογάριθμοι-Ιστορικά Στοιχεία
Λογαριθμικός Κανόνας
Λογαριθμικός Κανόνας
Για να δείτε το άρθρο πατήστε "Διαβάστε περισσότερα" ή επιλέξτε από
το μενού "Μαθηματική Βιβλιοθήκη/Άρθρα Βιογραφίες" και στη συνέχεια
την ενότητα "Μαθηματικά Άρθρα"
Η έννοια του λογαρίθμου επινοήθηκε στις αρχές του 17ου αιώνα ως ένα μέσο απλοποίησης των αριθμητικών υπολογισμών και η εμφάνισή των πρώτων λογαριθμικών πινάκων είχε, εκείνη την εποχή, επίπτωση στην επιστήμη ανάλογη με αυτή που έχουν οι ηλεκτρονικοί υπολογιστές στις μέρες μας. Η αρχική μαθηματική ιδέα στην οποία στηρίζεται η έννοια του λογαρίθμου είναι πολύ απλή. Αν θέσουμε σε αντιστοιχία ένα προς ένα τους όρους μιας αριθμητικής και μιας γεωμετρικής προόδου, όπως για παράδειγμα:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ...
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, ...
τότε μπορούμε να παρατηρήσουμε ότι το γινόμενο 2 όρων της γεωμετρικής προόδου (π.χ 32 x 128=4096) βρίσκεται ακριβώς κάτω από το άθροισμα των αντίστοιχων όρων της αριθμητικής (5+7=12).
Δηλαδή ο πολλαπλασιασμός ανάγεται ουσιαστικά σε πρόσθεση. Εύκολα μπορούμε επίσης να διαπιστώσουμε ότι η διαίρεση ανάγεται σε αφαίρεση, η ύψωση σε δύναμη σε πολλαπλασιασμό με τον εκθέτη και η εξαγωγή ρίζας σε διαίρεση με το δείκτη, όπως για παράδειγμα:
Όπως είναι φανερό, οι προηγούμενες αναγωγές στηρίζονται στις ιδιότητες των δυνάμεων (οι παραπάνω πρόοδοι είναι οι ακολουθίες των εκθετών και των αντίστοιχων δυνάμεων του 2 ή, με άλλα λόγια, οι όροι της αριθμητικής είναι οι λογάριθμοι των αντίστοιχων όρων της γεωμετρικής με βάση το 2). Το 16ο αιώνα όμως δεν υπήρχε κάποιος κοινά αποδεκτός συμβολισμός για τις δυνάμεις, ούτε είχαν διατυπωθεί με γενικότητα οι ιδιότητές τους. Το πρόβλημα που τέθηκε στους μαθηματικούς της εποχής ήταν η κατασκευή γεωμετρικών προόδων αρκετά «πυκνών», ώστε ανάμεσα στους όρους τους να μπορούν να παρεμβληθούν, χωρίς σημαντικό σφάλμα, οι αριθμοί που εμφανίζονταν συχνά στους υπολογισμούς (π.χ. οι τιμές των τριγωνομετρικών συναρτήσεων). Ταυτόχρονα οι όροι μιας τέτοιας προόδου θα έπρεπε να τεθούν σε ένα προς ένα αντιστοιχία με τους όρους μιας αριθμητικής προόδου.
Η κατασκευή πινάκων τέτοιων προόδων ήταν για την εποχή εκείνη έργο τεράστιο που η ολοκλήρωσή του απαίτησε πολλά χρόνια. Οι πρώτοι που δημοσίευσαν τέτοιους πίνακες ήταν ο Ελβετός Jost Burgi (1552-1632) και ο Σκωτσέζος John Napier (1550-1617). Ο Burgi ήταν ωρολογοποιός, κατασκευαστής αστρονομικών οργάνων και εργάστηκε στα μεγαλύτερα αστεροσκοπεία της εποχής του, ενώ ο Napier ήταν πλούσιος ευγενής με έντονο ενδιαφέρον για τα Μαθηματικά και τις εφαρμογές τους. Οι πίνακες προόδων του Burgi δε γνώρισαν μεγάλη διάδοση γιατί δημοσιεύθηκαν αργά (το 1620 στην Πράγα), όταν είχαν ήδη προηγηθεί, το 1614, οι αντίστοιχοι πίνακες του Napier οι οποίοι στην πράξη ήταν πιο χρήσιμοι. Στον Napier επίσης οφείλεται η δημιουργία του όρου «λογάριθμος» από τη σύνθεση των Ελληνικών λέξεων «λόγος» και «αριθμός». Η σημασία του όρου στο βιβλίο του « Περιγραφή του θαυμάσιου κανόνα των λογαρίθμων » ήταν: «ο αριθμός που μετρά το πλήθος των λόγων». Αν θεωρήσουμε για παράδειγμα τις προόδους:
0, 1, 2, 3, 4, 5, 6, 7, ...
1, 2, 4, 8, 16, 32, 64, 128, ...
τότε, ο 6 π.χ. (που είναι ο λογάριθμος του 64 με βάση το 2), δείχνει «πόσοι λόγοι» χρειάζονται στη συνεχή αναλογία:
Τέλος, το σύστημα προόδων του Burgi ισοδυναμεί, με ικανοποιητική προσέγγιση, με το σημερινό σύστημα των φυσικών λογαρίθμων που έχουν ως βάση τον αριθμό «e» ( e = 2,71828459045 ). (Το σύμβολο “e” χρησιμοποιήθηκε για πρώτη φορά από το Leonard Euler το 1728, έναν αιώνα μετά την εμφάνιση των λογαρίθμων).
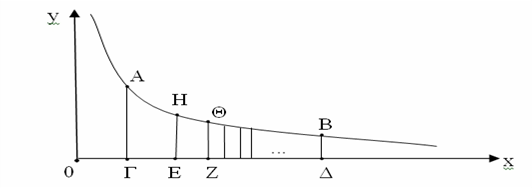
Ενώ λοιπόν οι λογάριθμοι είχαν, αρχικά, επινοηθεί αποκλειστικά για την απλοποίηση αριθμητικών υπολογισμών, γύρω στο 1650 διαπιστώθηκε μια απροσδόκητη εμφάνισή τους σε γεωμετρικά ζητήματα. Αφετηρία υπήρξε το πρόβλημα του υπολογισμού του εμβαδού που περικλείεται από ένα τόξο ΑΒ της υπερβολής
Έχουμε δηλαδή τη βασική αρχή ενός λογαριθμικού συστήματος, του οποίου όμως οι λογάριθμοι (όροι της αριθμητικής προόδου) έχουν εδώ μια προφανή φυσική σημασία: εκφράζουν τα εμβαδά συγκεκριμένων γεωμετρικών σχημάτων. Ο πρώτος που χρησιμοποίησε τον όρο «φυσικός λογάριθμος» ήταν ο N. Mercator (1620-1687) και αυτοί ακριβώς είναι οι σημερινοί λογάριθμοι με βάση το e που συμβολίζονται διεθνώς με το σύμβολο “ln” (από τα αρχικά των λέξεων “logarithmus naturalis”).
Στη σημερινή εποχή των ηλεκτρονικών υπολογιστών, η αρχική χρησιμότητα των λογαρίθμων ως ένα μέσο απλοποίησης των αριθμητικών υπολογισμών έχει φυσικά εκμηδενιστεί. Αντίθετα όμως, είναι πολύ μεγάλη η χρησιμότητα της εκθετικής και της λογαριθμικής συνάρτησης ως ένα μέσο μαθηματικής περιγραφής καταστάσεων του φυσικού κόσμου. Πολλές από τις εφαρμογές τους στηρίζονται στην αρχική ιδέα της αντιστοιχίας μιας γεωμετρικής και μιας αριθμητικής προόδου.
Πηγή :Ανδρεαδάκης-Κατσαργύρης-Παπασταυρίδης-Πολύζος-Σβέρκος:
Άλγεβρα Β’ Λυκείου, Ινστιτούτο τεχνολογίας υπολογιστών και εκδόσεων"Διόφαντος", Έκδοση 2013.
Ιστορία του Λογαρίθμου
Τον 16ο – 17ο αιώνα παρατηρήθηκε μια σημαντική ανάπτυξη της επιστημονικής γνώσης σε όλους τους κλάδους. Οι ανακαλύψεις των νέων χωρών, ο γύρος του κόσμου από τον Μαγγελάνο και η ανάπτυξη του ναυτικού εμπορίου δημιούργησαν την ανάγκη παραγωγής χαρτών (Gerhard Mercator, 1596). Η εισβολή των μαθηματικών στην αστρονομία και στη φυσική μετά τον Κοπέρνικο, τον Γαλιλαίο και τον Κέπλερ καθώς και το πλήθος των δεδομένων που προέκυψαν προς επεξεργασία στις προαναφερόμενες επιστήμες, απαιτούσαν από τους επιστήμονες τη διεκπεραίωση περίπλοκων υπολογισμών. Έπρεπε να επινοηθούν τρόποι που θα τους απάλλασσαν από αυτό το βάρος. Και επειδή είναι ευκολότερο να προσθέτουμε παρά να πολλαπλασιάζουμε, βρέθηκε τρόπος μετατροπής της πρόσθεσης σε πολλαπλασιασμό , ο λογάριθμος.O John Napier (1550-1617), 8ος Λόρδος του Merchistoun στη Σκωτία, γνωστός για τα θρησκευτικού περιεχομένου βιβλία του, ήταν ο πρώτος που, δεχόμενος την πρόκληση μετατροπής μιας πράξης σε μια άλλη πιο απλή, παρατήρησε τη σχέση των όρων μιας γεωμετρικής προόδου και των αντίστοιχων εκθετών τους, που ακολουθούν αριθμητική πρόοδο.
Ο Napier παίρνοντας ως βάση τον αριθμό 1-10-7 υποστήριξε ότι κάθε θετικός αριθμός Ν μπορεί να γραφεί ως Ν=107(1-10-7)L.
Έτσι έχουμε τον πρώτο ορισμό του Νεπέριου λογάριθμου: L=Nap logΝ.
Επί 20 χρόνια συμπλήρωνε τους διαδοχικούς όρους της γεωμετρικής προόδου που κατασκεύασε συγκεντρώνοντας τους τελικά στο έργο του Mirifici Logarithmorum Canonis Descriptio.
Παρατήρηση: Εδώ εμφανίζεται και για πρώτη φορά η τιμή της ακολουθίας
όταν το ν είναι πάρα πολύ μεγάλο, ως βάση για λογαρίθμους.
Το χρήμα είναι μαθηματικά
Τον 17ο αιώνα κάποιος ανώνυμος έμπορος ή τοκογλύφος παρατήρησε μια παράξενη συμπεριφορά στην αύξηση του τόκου στις τραπεζικές συναλλαγές, που στηρίζονται σε ανατοκισμό με ετήσιο επιτόκιο διαιρεμένο σε ν ίσα μέρη, όταν ο αριθμός ν είναι πάρα πολύ μεγάλος. Ας παρακολουθήσουμε το φαινόμενο:
Το χρήμα είναι μαθηματικά
Τον 17ο αιώνα κάποιος ανώνυμος έμπορος ή τοκογλύφος παρατήρησε μια παράξενη συμπεριφορά στην αύξηση του τόκου στις τραπεζικές συναλλαγές, που στηρίζονται σε ανατοκισμό με ετήσιο επιτόκιο διαιρεμένο σε ν ίσα μέρη, όταν ο αριθμός ν είναι πάρα πολύ μεγάλος. Ας παρακολουθήσουμε το φαινόμενο:
Η συνήθης τραπεζική μέθοδος αύξησης του δανειζόμενου κεφαλαίου είναι ο:
Ανατοκισμός
Έστω ότι καταθέτουμε € Κ σε ένα λογαριασμό που αποδίδει ε% ετήσιο επιτόκιο και ανατοκίζεται κάθε χρόνο.
Τέλος του 1ου έτους
Τέλος του Νου έτους :
Άλλη συνήθης τραπεζική συναλλαγή είναι ο:Ανατοκισμός ν φορές τον χρόνο με ετήσιο επιτόκιο διαιρεμένο σε ν ίσα μέρη
Δηλαδή, αν καταθέσουμε € 100 σε ένα λογαριασμό που αποδίδει 5% και τοκίζεται κάθε χρόνο:
Τέλος του 1ου έτους: € 105,00
Αν καταθέτουμε €100 σε ένα λογαριασμό που αποδίδει 5% τον χρόνο και
ανατοκίζεται κάθε εξάμηνο σε ένα χρόνο ανατοκίζεται δύο (2) φορές με επιτόκιο 2,5%
Τέλος 1ου έτους: 105,06
ανατοκίζεται κάθε τρίμηνο σε ένα χρόνο ανατοκίζεται τέσσερις (4) φορές με επιτόκιο 1,66%
Τέλος 1ου έτους: 105,09 €
ανατοκίζεται κάθε μήνα σε ένα χρόνο ανατοκίζεται δώδεκα (12) φορές με επιτόκιο
0,416%.
 %.
Τέλος 1ου έτους
%.
Τέλος 1ου έτους

Το e ως όριο
Ο αριθμός e, όπως διαπιστώσαμε, είναι όριο της ακολουθίας.
Ο τετραγωνισμός της υπερβολής
O Gregorius de Saint-Vincent (1584-1667), στην προσπάθεια τετραγωνισμού της υπερβολής, διαπιστώνει ότι, αν οι τετμημένες της γραφικής παράστασης της συνάρτησης μεταβάλλονται με γεωμετρική πρόοδο, τότε το εμβαδόν που βρίσκεται μεταξύ του άξονα των τετμημένων και της υπερβολής μεταβάλλεται με αριθμητική πρόοδο..
Όταν το e συναντά το φ: Λογαριθμική έλικα
Ο Jacob Bernoulli (1654-1705) μελέτησε τη λογαριθμική έλικα και την ονόμασε spira mirabilisλόγω των σπανίων μαθηματικών ιδιοτήτων της, που την καθιστούν, μετά τον κύκλο, το πιο προσφιλές διακοσμητικό μοτίβο.
Η λογαριθμική έλικα περιγράφεται ως καμπύλη με αφετηρία ένα σημείο (τον πόλο) και ανελίσσεται με τρόπο ώστε η απόσταση των σημείων της από το πόλο να αυξάνει με γεωμετρική πρόοδο, εφόσον η γωνία περιστροφής αυξάνει με αριθμητική πρόοδο. Κάθε ευθεία που διέρχεται από τον πόλο τέμνει την έλικα υπό την ίδια γωνία.
ανατοκίζεται κάθε εξάμηνο σε ένα χρόνο ανατοκίζεται δύο (2) φορές με επιτόκιο 2,5%
Τέλος 1ου έτους: 105,06
ανατοκίζεται κάθε τρίμηνο σε ένα χρόνο ανατοκίζεται τέσσερις (4) φορές με επιτόκιο 1,66%
Τέλος 1ου έτους: 105,09 €
ανατοκίζεται κάθε μήνα σε ένα χρόνο ανατοκίζεται δώδεκα (12) φορές με επιτόκιο
0,416%.
Τέλος 1ου έτους: 105,12 €
ανατοκίζεται κάθε ημέρα σε ένα χρόνο ανατοκίζεται τριακόσιες εξήντα
πέντε (365) φορές με επιτόκιο 0,0137 %
Τέλος 1ου έτους: 105,19 €
Έστω ότι ο ανατοκισμός γίνεται ν φορές τον χρόνο. Για κάθε περίοδο μετατροπής ως επιτόκιο
ανατοκίζεται κάθε ημέρα σε ένα χρόνο ανατοκίζεται τριακόσιες εξήντα
πέντε (365) φορές με επιτόκιο 0,0137 %
Τέλος 1ου έτους: 105,19 €
Έστω ότι ο ανατοκισμός γίνεται ν φορές τον χρόνο. Για κάθε περίοδο μετατροπής ως επιτόκιο
θεωρείται το ετήσιο επιτόκιο διαιρεμένο με τον ν, δηλαδή
Παρατήρηση: Το τελικό κεφάλαιο για περίοδο μετατροπής πάρα πολύ μικρή, π.χ .
 , δεν ξεπερνά το 2,72 του αρχικού κεφαλαίου.
, δεν ξεπερνά το 2,72 του αρχικού κεφαλαίου.
Παρατηρούμε ότι ο τύπος 
πλησιάζει μια τιμή χωρίς να τη φτάνει και αυτή είναι ο αριθμός e. Τότε λέμε ότι η ακολουθία με τύπο  έχει όριο τον αριθμό e.
έχει όριο τον αριθμό e.
Το e ως όριο
Ο αριθμός e, όπως διαπιστώσαμε, είναι όριο της ακολουθίας.
Αλλά, αφού για μεγάλες τιμές του ν η τιμή του  θα είναι σχεδόν μηδέν,
θα είναι σχεδόν μηδέν,
έχουμε:
Συνεπώς
O Gregorius de Saint-Vincent (1584-1667), στην προσπάθεια τετραγωνισμού της υπερβολής, διαπιστώνει ότι, αν οι τετμημένες της γραφικής παράστασης της συνάρτησης μεταβάλλονται με γεωμετρική πρόοδο, τότε το εμβαδόν που βρίσκεται μεταξύ του άξονα των τετμημένων και της υπερβολής μεταβάλλεται με αριθμητική πρόοδο..
Όταν το e συναντά το φ: Λογαριθμική έλικα
Ο Jacob Bernoulli (1654-1705) μελέτησε τη λογαριθμική έλικα και την ονόμασε spira mirabilisλόγω των σπανίων μαθηματικών ιδιοτήτων της, που την καθιστούν, μετά τον κύκλο, το πιο προσφιλές διακοσμητικό μοτίβο.
Η λογαριθμική έλικα περιγράφεται ως καμπύλη με αφετηρία ένα σημείο (τον πόλο) και ανελίσσεται με τρόπο ώστε η απόσταση των σημείων της από το πόλο να αυξάνει με γεωμετρική πρόοδο, εφόσον η γωνία περιστροφής αυξάνει με αριθμητική πρόοδο. Κάθε ευθεία που διέρχεται από τον πόλο τέμνει την έλικα υπό την ίδια γωνία.
Οι λογάριθμοι
Η ιδέα των λογαρίθμων γεννήθηκε πιθανόν από τους αστρονόμους οι οποίοι έπρεπε να πολλαπλασιάζουν και να διαιρούν πολύπλοκες τριγωνομετρικές ποσότητες. Στο μεταξύ οι πίνακες με τους αριθμούς και τις δυνάμεις έδειχναν ότι ο πολλαπλασιασμός στον ένα πίνακα αντιστοιχούσε σε πρόσθεση στον άλλο. Στην αυγή του 17ου αιώνα ο σκωτσέζος John Napier ήNeper είχε την ιδέα της δημιουργίας ενός πίνακα λογαρίθμων ο οποίος θα διευκόλυνε τους πολλαπλασιασμούς οποιωνδήποτε ποσοτήτων ανάγοντάς τους σε προσθέσεις. Το 1617 δημοσίευσε τον σχετικό πίνακα και το όνομά του δημιούργησε αργότερα τον όρο “νεπέριοι λογάριθμοι”.
Σήμερα η έννοια λογάριθμος έχει διαφοροποιηθεί σε σχέση με εκείνη που πρότεινε Οο Neper.O λογάριθμος ενός αριθμού, όπως λόγου χάρη ο 50, είναι ο ΕΚΘΕΤΗΣ τον οποίο πρέπει να έχει o αριθμός e ( βάση ) ώστε να είναι ίσος με 50.
Λογαριθμικός Κανόνας
Στις αρχές του 17ου αιώνα για την εκτέλεση πράξεων επινοήθηκε και κατασκευάστηκε ο λογαριθμικός κανόνας, που στηρίζεται στις ιδιότητες των λογαρίθμων. Η επινόηση του αποδίδεται στον Άγγλο μαθηματικό E. Gunter, χωρίς να παραβλέπεται και η προσφορά των John Napier, L. Euler, Jobst Burgi και άλλων.
Χρησιμοποιήθηκε μέχρι τα μέσα της δεκαετίας του 1970, όπου εμφανίστηκαν στην αγορά οι αριθμομηχανές, τα κομπιουτεράκια.
Ο λογαριθμικός κανόνας μπορεί να θεωρηθεί πρόδρομος των ηλεκτρονικών υπολογιστών.
Δείτε ένα σχετικό βίντεο που εξηγεί την χρήση του.
Πηγή: http://mathmosxos.blogspot.gr/
http://mathhmagic.blogspot.gr/