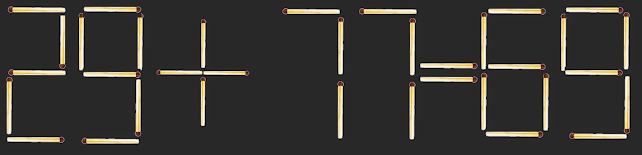neo

ΚΚ

Μαθηματικοί Γρίφοι-Ασκήσεις με ασυνήθιστη εκφώνηση




Συνεχής Ανανέωση

Γρίφος 1
Ο Κώστας συναντά τον φίλο του Γιάννη και ακούγεται ο διάλογος:
Κ: Πόσα παιδιά έχεις;
Γ: Τρία.
Κ: Πόσων χρονών είναι;
Γ: Το γινόμενο των ηλικιών τους είναι 36.
Κ: Δεν μου λες τίποτα με αυτό.
Γ: Το άθροισμα των ηλικιών τους είναι όσο ο αριθμός  της απέναντι πολυκατοικίας.
Κ: Την πολυκατοικία την βλέπω, αλλά πάλι δεν μου λες τίποτα.
Γ: Ε, σου λέω ότι το μικρό μου παιδί έχει πράσινα μάτια.
Κ: Τώρα μάλιστα. Ξέρω πόσων χρονών είναι το κάθε σου παιδί.
Πόσων χρονών είναι το κάθε παιδί;

 Λύση

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 2
Μόλις έχω μετακομίσει σε διαμέρισμα του 5ου ορόφου πολυκατοικίας,η οποία έχει 7 ορόφους και κάθε όροφος 3 διαμερίσματα.
Τα κουδούνια στην είσοδο της πολυκατοικίας είναι ανακατεμένα και εγώ δεν ξέρω ποιο αντιστοιχεί στο δικό μου θυροτηλέφωνο.
Είμαι μόνος μου και έχω στη διάθεσή μου μόνο ένα κασετόφωνο και μια άγραφη κασέτα.
Πως μπορώ να εντοπίσω το κουδούνι που αντιστοιχεί στο διαμέρισμά μου;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 3
Πως είναι δυνατόν 2 πατέρες και 2 γιοί να μοιρασθούν 21 κέρματα του ενός ευρώ εξ ίσου μεταξύ τους

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 4
Το άθροισμα των ηλικιών δυο αδελφών είναι 11 έτη. Ο ένας είναι 10 χρόνια μεγαλύτερος από τον άλλον. Ποιες είναι οι ηλικίες τους;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 5
Ένας κλέφτης μπαίνει σε ένα χωράφι και κλέβει ένα πανέρι πορτοκάλια. Στον δρόμο τον βλέπει ένας χωρικός και του λέει πως για να μην τον καρφώσει θα πρέπει να του δώσει τα μισά από τα πορτοκάλια που έχει στο πανέρι του και μισό πορτοκάλι ακόμα. Ο κλέφτης συμβιβάζεται και φεύγει.
Παρακάτω τον σταματάει και άλλος χωρικός και του λέει το ίδιο πράγμα.Θέλει τα μισά από τα πορτοκάλια που του έχουν απομείνει και μισό πορτοκάλι ακόμα. Ο κλέφτης τα δίνει και αυτά, αλλά παρακάτω πέφτει και σε τρίτο χωρικό ο οποίος του λέει πάλι το ίδιο.
Όταν ο κλέφτης δίνει και σε αυτόν τα πορτοκάλια που του ζητούσε, κοιτάζει μέσα στο πανέρι και βλέπει πως του έχει απομείνει μόνο ένα πορτοκάλι. 
Πόσα είχε κλέψει αρχικά; 

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~     
Γρίφος 6
Δίνονται 6 διαδοχικοί ακέραιοι. Οι 3 πρώτοι έχουν άθροισμα 27. Ποιο είναι το άθροισμα των 3 επόμενων;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 7
Το 215 π.Χ. τρία αδέρφια κληρονόμησαν από τον πατέρα τους 17 αγελάδες. Η διαθήκη του πατέρα έγραφε ότι ο Α πρέπει να πάρει τις μισές, ο Β το ένα τρίτο και ο Γ το ένα ένατο από αυτές. 
Πήγαν τότε στον Αρχιμήδη (287-212 π.Χ.) και τον παρακάλεσαν να τους βοηθήσει στη μοιρασιά, πράγμα που ο Αρχιμήδης έκανε,χωρίς να σφάξει αγελάδα και σεβόμενος απόλυτα τη διαθήκη του πατέρα. 
Πως έγινε αυτό;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 8
Τέσσερα άτομα πρέπει να διασχίσουν μια γέφυρα βράδυ με τη βοήθεια ενός φακού που έχουν μαζί τους.
Μπορούν να περνούν τη γέφυρα έως δυο άτομα. Καθένας από τους παραπάνω διασχίζει τη γέφυρα σε διαφορετικό χρόνο.
Δηλαδή:
ο πρώτος χρειάζεται τουλάχιστον 1 λεπτό,
ο δεύτερος χρειάζεται τουλάχιστον 2 λεπτά,
ο τρίτος χρειάζεται τουλάχιστον 5 λεπτά και
ο τέταρτος χρειάζεται τουλάχιστον 10 λεπτά.
Με ποιόν τρόπο θα μπορέσουν να περάσουν όλοι από το ένα άκρο της γέφυρας ως το άλλο σε 17 λεπτά;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 9
Ο Ανδρέας και ο Βασίλης έτρεξαν σε μια κούρσα 100 μέτρων. Όταν ο Ανδρέας τερμάτισε, ο Βασίλης βρισκόταν στα 90 μέτρα. Ο Ανδρέας πρότεινε στον Βασίλη να ξανατρέξουν αλλά αυτή τη φορά θα ξεκινούσε 10 μέτρα πίσω απ' τον Βασίλη για να είναι πιο αμφίρροπο το αποτέλεσμα. Αν κρατηθούν όλες οι άλλες συνθήκες ίδιες, θα κερδίσει ο Ανδρέας, ο Βασίλης ή θα τερματίσουν ταυτόχρονα;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 10
Ένας φυλακισμένος δραπέτευσε από τη φυλακή και φεύγοντας συναντάει μπροστά του μια διχάλα με δυο δρόμους.
Ξέρει ότι ο ένας από αυτούς οδηγεί ξανά πίσω στη φυλακή και ο άλλος έξω στην πόλη χωρίς όμως να μπορεί να τους ξεχωρίζει.
Ακριβώς στη διχάλα του δρόμου βρίσκονται δυο άνθρωποι από τους οποίους ο ένας λέει μόνο αλήθεια και ο άλλος μόνο ψέματα (και αυτό το γνωρίζουν και οι δυο).
Ο φυλακισμένος γνωρίζει ότι ο ένας από τους δυο λέει μόνο την αλήθεια αλλά δεν ξέρει ποιος.
Ποια είναι η ερώτηση που πρέπει να κάνει στον καθένα για να καταλάβει ποιος είναι ο δρόμος που οδηγεί στην πόλη;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 11
Έχουμε τρία ξυλάκια στη σειρά, όπως στο σχήμα: l l l. Πως μπορούμε με μια μόνο κατάλληλη μετακίνηση να δημιουργήσουμε έναν αριθμό μικρότερο του 4 και μεγαλύτερο του 3;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 12
Στα πλαίσια ενός προγράμματος ανακύκλωσης, όσοι επιστρέφουν άδεια μπουκάλια κάποιου αναψυκτικού μπορούν να τα ανταλλάξουν µε γεμάτα. Συγκεκριμένα, τα 4 άδεια μπουκάλια ανταλλάσσονται µε 1 γεμάτο. 
Πόσα μπουκάλια αναψυκτικού θα πιει μια οικογένεια που συγκέντρωσε 24 άδεια μπουκάλια;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 13

 
               Ποιος αριθμός λείπει από την πυραμίδα;


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 14
Να βρείτε ποιοι θετικοί ακέραιοι αριθμοί πρέπει να τοποθετηθούν στα κενά του παρακάτω πίνακα ώστε:
⦁ Το γινόμενο των τριών πρώτων κελιών (από αριστερά) να ισούται με 30
⦁ Το γινόμενο των τριών μεσαίων να είναι 90
⦁ Το γινόμενο των τριών τελευταίων να είναι 360
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 15
Κάποιος φιλάνθρωπος προσέφερε ως δωρεά τα κάτωθι ποσά:
⦁ Σε μια φτωχή οικογένεια προσέφερε ως δωρεά 1 ευρώ παραπάνω από τα μισά από όσα είχε αρχικά στο πορτοφόλι του.
⦁ Σ' ένα ορφανό που ζητιάνευε προσέφερε 2 ευρώ παραπάνω από τα μισά όσων χρημάτων είχαν μείνει στο πορτοφόλι του.
⦁ Τέλος σε μια ζητιάνα προσέφερε 3 ευρώ παραπάνω από τα μισά χρήματα που είχαν μείνει στο πορτοφόλι του.
Όταν έφτασε στο σπίτι του είδε πως στο πορτοφόλι του είχε μείνει μόλις 1 ευρώ.
Πόσα χρήματα είχε στην αρχή;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 16
Από 10 σακιά λίρες , το ένα μόνο περιέχει κάλπικες, που ζυγίζουν 2 γραμμάρια η μία , ενώ οι γνήσιες ζυγίζουν 3 γραμμάρια η μία. 
Πως μπορούμε με μια μόνο ζύγιση , να βρούμε το σακί με τις κάλπικες λίρες.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 17
Ο διαιρετέος μιας διαίρεσης είναι 417 και το πηλίκο 12. Αν ο διαιρετέος , ο διαιρέτης και το υπόλοιπο πολλαπλασιασθούν επί 3 , τότε το άθροισμα του πηλίκου και του υπολοίπου  αυξάνεται κατά 18. Ποιος είναι ο διαιρέτης;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 18
Το άλμα της αλεπούς είναι 1 m και του σκύλου 2 m.Αλλά ο σκύλος κάνει 2 άλματα , όταν η αλεπού κάνει 3.
Σκύλος βρίσκεται στη θέση Α και κυνηγάει αλεπού που βρίσκεται 30 m μπροστά του.Σε ποια απόσταση από τη θέση Α θα τη φθάσει;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 19
Φράκτης περικλείει ένα τετράγωνο. Οι οκτώ στύλοι κάθε πλευράς έχουν πάχος 6 cm και απέχουν μεταξύ τους 6 m.Πόσοι είναι στύλοι και πόσο το εμβαδόν του τετραγώνου;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 20
Έχουμε 9 κέρματα και ξέρουμε ότι το ένα ζυγίζει λιγότερο από τα άλλα. Έχουμε επίσης μια ζυγαριά χωρίς σταθμά. Πως με δυο ζυγίσεις θα βρούμε το κάλπικο κέρμα;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 21
Στο παρακάτω σχήμα ,το τετράγωνο ΑΖΔΓ περιέχει δύο τετράγωνα , το ΑΗΚΒ με εμβαδό Ε1=16 τ.μ και το ΗΖΕΘ με εμβαδό Ε2=9 τ.μ.
Να βρείτε την περίμετρο του σχήματος ΒΓΔΕΘΚ
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 22
Η απόσταση της Θεσσαλονίκης από την Αθήνα είναι 540 km. Δύο τρένα ξεκινούν από τις δύο πόλεις και κινούνται αντίθετα  μέχρι να συναντηθούν. Το ένα κινείται με ταχύτητα 130 km/h και το άλλο με ταχύτητα 140 km/h. Ένα χελιδόνι πετά με ταχύτητα 240 km/h και ξεκινά από το ένα τρένο , πάει βρίσκει το άλλο , ξαναγυρνάει στο πρώτο τρένο κ.ο.κ. Όταν συναντηθούν τα δύο  τρένα τι απόσταση θα έχει διανύσει το χελιδόνι;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 23
Αυτοκίνητο μήκους 10 m κινείται με ταχύτητα 50 km/h και μπροστά του βρίσκεται νταλίκα μήκους 25 m που κινείται με ταχύτητα 45 km/h. Πόσα δευτερόλεπτα θα χρειαστεί το αυτοκίνητο για να προσπεράσει την νταλίκα;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 24
Στο σπίτι του διπλανού σχήματος η στέγη είναι ισοσκελές τρίγωνο. Το μήκος των δύο πλευρών της ισοσκελούς στέγης είναι 5 m και η βάση του σπιτιού είναι 8 m.
Ποιο είναι το εμβαδόν της στέγης;



~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 25
Η διαφορά των τετραγώνων δύο διαδοχικών ακέραιων αριθμών  είναι 199. Να βρείτε το άθροισμα των τετραγώνων των δύο αυτών διαδοχικών αριθμών.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 26
Στο διπλανό σχήμα , καθένα από τα δύο τετράγωνα έχει τέσσερα κοινά σημεία με τον κύκλο. Για να καλύψουμε την επιφάνεια του εξωτερικού τετραγώνου με χρειαζόμαστε 100 ίδια πλακίδια. Με πόσα ίδια πλακίδια θα καλύψουμε την επιφάνεια του εσωτερικού τετραγώνου;




~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 27
Να βρείτε τον αριθμό του οποίου το τετράγωνο και ο κύβος περιέχουν όλα τα ψηφία από το 0 έως και το 9 από μια φορά το καθένα.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 28
Δύο φίλοι παίζουν το παιχνίδι  ¨ Άξονες Συντεταγμένων¨. Στόχος τους είναι είναι να οριοθετήσουν την περιοχή που καθορίζει ο αρχηγός του παιχνιδιού. Ο αρχηγός είπε: 
''Βρείτε την τομή των συνόλων Α και Β του επιπέδου με Α={(x,y):|x-2|<3}  και Β={(x,y): |y|<5}''

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 29
Από ένα γκρουπ 100 τουριστών, οι 90 επισκέφθηκαν το Αρχαιολογικό Μουσείο, οι 90 το Βυζαντινό Μουσείο και οι 90 το Λαογραφικό Μουσείο. Ποιος είναι ο μικρότερος δυνατός αριθμός τουριστών που επισκέφθηκαν και τα τρία αυτά αξιοθέατα;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 30
Στο παρακάτω σχήμα παρουσιάζονται τα σπίτια ενός δρόμου. Τα σπίτια είναι κτισμένα το ένα ακριβώς δίπλα από το άλλο, χωρίς να υπάρχουν κενά. Τα σπίτια στις δύο πλευρές του δρόμου είναι ακριβώς το ένα απέναντι από το άλλο. Η αρίθμηση των σπιτιών αρχίζει από τη μια πλευρά του δρόμου και συνεχίζει στην απέναντι πλευρά.
Το σπίτι που βρίσκεται ακριβώς απέναντι από το σπίτι με τον αριθμό 1 έχει το μεγαλύτερο αριθμό.
Τα σπίτια με αριθμό 9 και 34 βρίσκονται ακριβώς απέναντι το ένα από το άλλο, όπως φαίνεται στο σχήμα.
Πόσα σπίτια βρίσκονται συνολικά και στις δύο πλευρές του δρόμου;




~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 31
Αριθμητική  με σπίρτα
α. Αφαιρέστε ένα σπίρτο και μετακινείστε άλλο ένα ώστε να ισχύει η ισότητα:


Λύση

β. Μετακινείστε ένα σπίρτο ώστε να ισχύει η ισότητα:


Λύση

γ. Μετακινείστε δύο σπίρτα ώστε να ισχύει η ισότητα:



Λύση

δ. Μετακινείστε ένα σπίρτο ώστε να ισχύει η ισότητα:



Λύση

ε. Μετακινείστε δύο σπίρτα και προσθέστε ένα ώστε να ισχύει η ισότητα:




~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Γρίφος 32
Σπείρα με σπίρτα

Στην παρακάτω εικόνα βλέπετε μια αριστερόστροφη σπείρα κατασκευασμένη από 35 σπίρτα. Να δημιουργήσετε μια δεξιόστροφη σπείρα στρέφοντας 4 σπίρτα οριζόντια ή κατακόρυφα.



Λύση

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 33
Κατασκευή με σπίρτα
Στο παρακάτω σχήμα, έχουμε τοποθετήσει 16 σπίρτα. Μπορείτε, μετακινώντας μόνο 3 σπίρτα, να κατασκευάσετε τέσσερα ίσα τετράγωνα;


Λύση
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 34
Οι κόκκινες ταινίες , στο παρακάτω σχήμα, έχουν διπλάσιο μήκος από τις μπλε. Πως μπορούμε να τις τοποθετήσουμε στο επίπεδο χωρίς να τις κόψουμε ή να τις διπλώσουμε έτσι ώστε να σχηματίσουμε τρία ισεμβαδικά τετράγωνα;



~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 35
Κατασκευή με σπίρτα
Στο παρακάτω σχήμα, έχουμε τοποθετήσει 14 σπίρτα. Μπορείτε, μετακινώντας μόνο 2 σπίρτα, να φτιάξετε  2 τετράγωνα;



~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 36
Μετακινήστε μόνο έναν σπίρτο έτσι ώστε η παρακάτω εξίσωση να γίνει σωστή

Λύση

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 37
Στο παρακάτω σχήμα μετακινήστε 2 σπίρτα για να σχηματίσετε 3 τρίγωνα

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 38
Στο παρακάτω σχήμα μετακινήστε 4 σπίρτα για να σχηματίσετε 3 τετράγωνα.


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 39
Στο παρακάτω σχήμα μετακινήστε 2 σπίρτα έτσι ώστε να σχηματίσετε 11 τετράγωνα


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 40
Συμπλήρωση πίνακα
Συμπληρώστε τον παρακάτω πίνακα, ώστε το άθροισμα κάθε γραμμής και κάθε στήλης να είναι ίσο με τον αριθμό που φαίνεται στο εξωτερικό του.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 41
Σκεφτείτε έναν τριψήφιο αριθμό. Γράψτε στο κομπιουτεράκι σας αυτόν τον αριθμό δυο συνεχόμενες φορές. Π.χ αν σκεφτήκατε τον αριθμό 123 γράψτε 123123. Διαιρέστε τον αριθμό που έχετε στην οθόνη σας με το 7. Θα παρατηρήσετε ότι η διαίρεση είναι τέλεια δηλαδή δεν προκύπτουν δεκαδικά ψηφία. Διαιρέστε τον νέο αριθμό που έχετε στην οθόνη σας με το 11. Πάλι η διαίρεση είναι τέλεια. Διαιρέστε τον νέο αριθμό με το 13 . Και πάλι η διαίρεση είναι τέλεια και μάλιστα έχετε καταλήξει στον αρχικό σας αριθμό. 
Μπορείτε να αποδείξετε ότι όλα τα παραπάνω ισχύουν για οποιονδήποτε τριψήφιο αριθμό;


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 42
Στην παρακάτω σκάλα, για την προστασία των μαθητών πρέπει να τοποθετηθεί ένα προστατευτικό ξύλο από το σημείο Α στο σημείο Β. Κάθε σκαλοπάτι έχει ύψος 10 cm και πλάτος 20 cm.
Πόσο είναι το μήκος του προστατευτικού ξύλου;


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 43
Υπάρχουν οκτώ μαθητές που κάθονται σε κύκλο στις θέσεις Μ1 έως Μ8 όπως φαίνεται στο διπλανό σχήμα.
Κάθε μαθητής έχει ένα αριθμό από το 1 έως το 8. Κάθονται όμως σε τυχαία σειρά (όχι σύμφωνα με τον αριθμό τους)
Όλοι οι μαθητές γνωρίζουν τους αριθμούς των άλλων. Ο καθηγητής τους προσπαθεί να βρει ποιον αριθμό έχει ο κάθε μαθητής.
Ο μαθητής στη θέση Μ1 λέει ότι: ¨ η άθροιση των αριθμών των άμεσων γειτόνων είναι 14¨
Αντίστοιχα οι μαθητές από την θέση Μ3 ως την θέση Μ8 απαντούν 15, 6, 12, 7, 11, 4.
Βοηθήστε τον καθηγητή να βρει ποιος αριθμός αντιστοιχεί σε κάθε μαθητή.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 44
Υπάρχουν 4 πόρτες. Πίσω από μία πόρτα βρίσκεται ένας θησαυρός. Μπροστά από τις πόρτες βρίσκονται 4 φύλακες. Από αυτούς ο ένας λέει την αλήθεια και όλοι οι άλλοι ψέματα. 


A: Ο φύλακας της πόρτας Α λέει πως ο θησαυρός είναι είτε πίσω από την πόρτα Β είτε πίσω από την πόρτα Δ 
Β: Ο φύλακας της πόρτας Β λέει πως ο θησαυρός δεν είναι πίσω από την πόρτα Β 
Γ: Ο φύλακας της πόρτας Γ λέει πως ο θησαυρός είναι πίσω από την πόρτα Γ 
Δ: Ο φύλακας της πόρτας Δ λέει πως ο θησαυρός είναι είτε πίσω από την πόρτα Α είτε πίσω από την πόρτα Γ 
Πίσω από ποια πόρτα βρίσκεται ο θησαυρός;
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 45
Στον  παρακάτω πίνακα, το άθροισμα κάθε γραμμής , κάθε στήλης και μιας διαγωνίου είναι 6. (όπως φαίνεται στο εξωτερικό του).Αλλάξτε τη θέση κάποιων αριθμών ώστε κάθε γραμμή, κάθε στήλη και οι δύο διαγώνιοι να έχουν άθροισμα πάλι 6  


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 46
Στον παρακάτω πίνακα, από ποιο τετράγωνο πρέπει να ξεκινήσετε για να διατρέξετε όλα;


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 47
Η Δημήτρια έχει πάνω στο γραφείο της μια λωρίδα χαρτιού και προσπαθεί να τη διπλώσει στη μέση. Σηκώνει το πάνω άκρο της, τη τσακίζει σε κάποιο σημείο που της φαίνεται κεντρικό και τη διπλώνει προς το κάτω άκρο. Βλέπει όμως πως από κάτω περισσεύουν 10 εκατοστά χαρτιού. 
Ανοίγει τη λωρίδα χαρτιού και πιάνει το κάτω άκρο , το τσακίζει σε ένα διαφορετικό σημείο και το διπλώνει στο πάνω άκρο. Όμως πάλι περισσεύουν 10 εκατοστά, αυτή τη φορά από την πάνω πλευρά της λωρίδας. Απογοητευμένη απλώνει τη λωρίδα χαρτιού στο γραφείο της, που τώρα έχει πάνω της τα ίχνη από δύο τσακίσεις. 
Πόσα εκατοστά απέχουν οι δύο τσακίσεις μεταξύ τους;

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 48
Το κάθε εικονιζόμενο σύμβολο αντιστοιχεί σε έναν αριθμό και με τις πράξεις ανάμεσά τους όλες οι εξισώσεις είναι σωστές.
Ποιος αριθμός μπαίνει στη θέση του ερωτηματικού;


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 49
Το κάθε εικονιζόμενο σύμβολο αντιστοιχεί σε έναν αριθμό και με τις πράξεις ανάμεσά τους οι εξισώσεις είναι σωστές.
Ποιος αριθμός μπαίνει στη θέση του ερωτηματικού;


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γρίφος 50

Ο κ. Κώστας αποφάσισε να κάνει δώρο  στην εγγονή του Δημήτρια ένα παιχνίδι με αριθμούς.

Έτσι κατασκεύασε τα εξάγωνα του παρακάτω σχήματος
Ο σκοπός είναι να τοποθετηθούν  τα εξάγωνα στο μεγάλο πλέγμα, έτσι ώστε εκεί όπου το ένα εξάγωνο ακουμπά το άλλο κατά μήκος της έντονης γραμμής, θα πρέπει και τα δύο τρίγωνα να έχουν το ίδιο περιεχόμενο. Δεν επιτρέπεται η περιστροφή κανενός εξαγώνου.
Μπορείτε να την βοηθήσετε την Δημήτρια;


Λύση

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~





~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx